Ieraksts rakstu sērijā lekciju pieraksti.

1.1 Kopas jēdziens

Def: kopa

Ar vārdu kopa mat. saprot, tādu jēdzienu, kuram var viennozīmīgi pateikt, ka kāds elements tai pieder vai nepieder

Kopas parasti apzīmē ar lielajiem latīņu burtiem

N – naturālie

Z – veselie

Q – racionālie

R – reālie

C – kompleksie

– tukšā kopa

Intervāli:

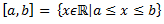
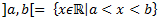
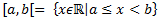
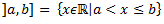
(a,b) – vektors – nevis intervāls

3.kopas, kur

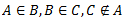
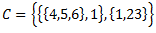
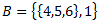
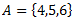
Uzdošanas veidi

• Ar elementu sarakstu (uzskaitot visus elementus)
  {a,b,c,d}
• Ar rakstīrīgo pazīmi (lielām/bezgalīgām kopām)

  

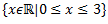
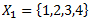
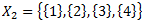
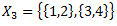
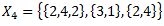
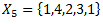
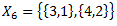
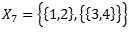
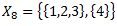
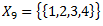
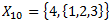
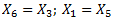
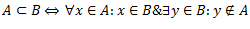
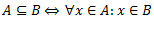
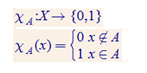
X – universs

Hi – kopas A harakteristiskā funkcija

1.2 Matemātiskās loģikas simboli

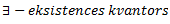
! (patiesībā izskatās, kā spoguļots lielais krievu G) – negācija

& – konjunkcija

V – disjunkcija

=> implikācija

<=> ekvivalence

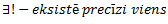
1.3 Darbības ar kopām

�

A, B – kopas

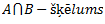
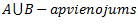
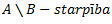
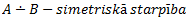
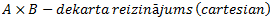
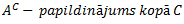
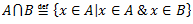
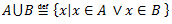
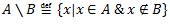
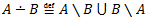
1.3.5 Operāciju īpašības

Operācijas tiks veiktas, ar operācijām A,B,C, kuras ir universālkopas X apakškopas1.

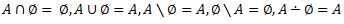
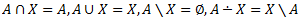
2.

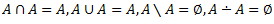
3.

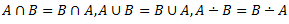
4.

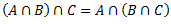
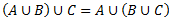
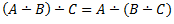
5.

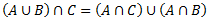
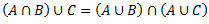
6.

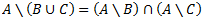
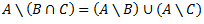
1.3.6 Kopas papildinājums

Kopas A papildinājums ir tie un tikai tie elementi, kas nepieder kopai A. (papildinājumam būtisks ir Universs, t.i. Kopa pret kuru tiek veikts papildinājums)

1.4 Kopu saimes

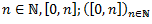
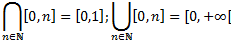
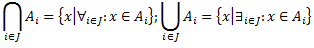
1.5 Dekarta reizinājums

1.5.1. Korteža jēdziens

Kortežs – sakārtota elementu virknīte (a,b,..)
(a,b) != {a,b} – iekš {a,b} secība nav svarīga, savukārt iekš korteža – secība ir svarīga.
Kortežu piemēri – Vektors, Matricas rinda, matricas kolonna.

1.5.2. Dekarta reizinājums

A,B – kopas

AxB = kopu A un B dekarta reizinājums

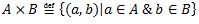
1.5.3. Dekarta reizinājuma īpašības

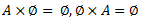
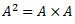
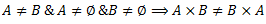
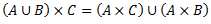
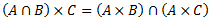
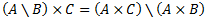
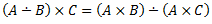
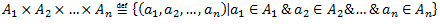
1.5 Funkcijas

1.6.1. Funkcijas vispārīga def.

X,Y – kopas, f – funkcija, Df – funkcijas definīcijas kopa

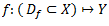
f ir likums, saskaņā ar kuru, katram funkcijas definīcijas kopas Df elementam x ir piekārtots viens kopas Y elements y, kuru apzīmē ar f(x) un sauc par funkcijas vērtību punktā x

X – funkcijas f starta kopa

Y – funkcijas f finiša kopa

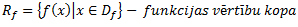
f- var uzdot ar tabulu (ja X & Y ir galīgas kopas), grafiku vai analītiski (f(x) = x2)

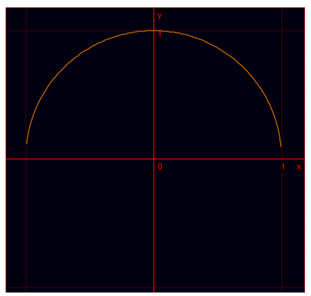
Grafiks ir kopa:

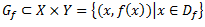
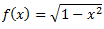
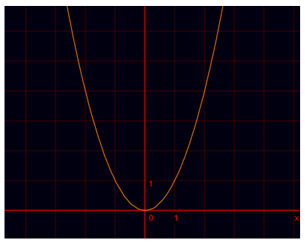
f(x) = x2

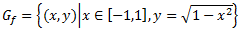
1.6.2. Funkciju klasifikācija

• Visur definēa funkcija <==> D_f =X
  
• Sirjekcija <==> R_f = Y
  
• Injekcija <==> visiem y no R_f eksistē viens vienīgs x no D_f, tāds, ka y=f(x)
  
• Bijekcija <==> visur definēta funkcija & injekcija & sirjekcija
• Ja X = R, Y – R, – viena argumenta (reālas) funkcijas
• Ja X = Rⁿ, Y -R, – vairāku argumentu (reālu) funkcijas
  Ja X = Rⁿ, Y -R^k – vairāku argumentu vektorfunkcijas
  
• Ja X = C, Y – C, – kompleksā mainīgā funkcijas
  

  Ja Df = N – tad tā ir skaitļu virkne (a1,a2, …, an) – reāla viena argumenta funkciju speciālgadījums

Pamatelementārās funkcijas

1. Konstantes
   f(x) = C, kur C = ir reāls skaitlis – Df = R
2. Pakāpes f-jas
   f(x)=x^r Df – atkarīgs no r – ja r = 2 – Df = R, r = 1/2 – Df = R \ {0},
3. Eksponentfunkcijas
   f(x) = a^x
   a!= 1 & a>0
4. Logaritmiskās f-jas
   f(x)=log_a(x)
   a!= 1 & a>0
5. Trigonometriskās funkcijas
   f(x) = sin(x)| cos(x)| tg(x)| ctg(x)
6. Inversās trigonometriskās funkcijas
   f(x) = arcSin(x)|arcCos(x)|arcTg(x)|arcCtg(x)
7. Ciklometriskās funkcijas
   f(x) = sinh(x)|cosh(x)|tanh(x)|ctanh(x)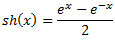

   
   Funkciju var iegūt no pamatelementārām funkcijām izmantojot galīgā skaitā operācijas + – * / kompozīcija

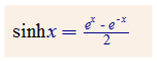
1.6.3. Viena reāla argumenta funkciju pamatīpašības

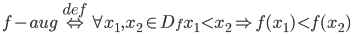
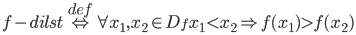
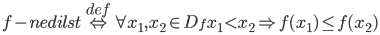
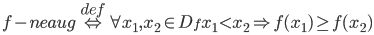
f- monotona <=> (f – nedilst) V (f – nedilst)

f – st. monotona <=> (f – aug) V (f -dilst)

f- ierobežota no augšas <=>

f- ierobežota no apakšas <=>

f – ierobežota <=> f – ierobežota no augšas & f -ierobežota no apakšas

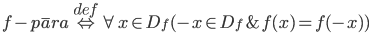
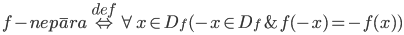
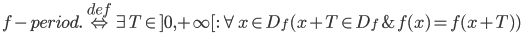
1.6.4. Saliktas funkcijas jēdziens

Piemēri:

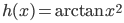
1.6.5. Inversās funkcijas jēdziens

X,Y – kopas

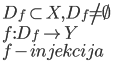
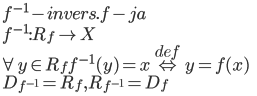
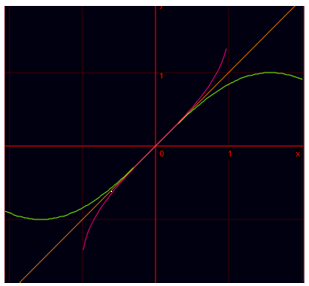
1.6.6. Attēli un pirmtēli

f(A) – kopas attēls

f-1(B) – kopas B pirmtēls

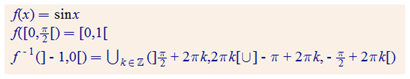
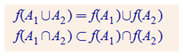
1.7. Kopas apjoms

1.7.1. Ekvivalentas kopas

A,B – kopas

1.7.2. Galīgas un bezgalīgas kopas

cardA, |A| – kopas elementu skaits

|tukša kopa| = 0

A ~ {1,2,3,…,n} => |A|= n

Kardinālskaitļi

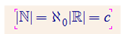
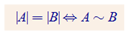
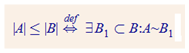
Ja kopas A un B ir galīgas, tad apvienojums, šķēlums, starpība utt. ir galīgas kopas

Ja A un B ir bezgalīgas, tad apvienojums ir bezgalīgs, bet par pārējām op. neko nevar pateikt

Ja A – galīga un B bezgalīga, tad apvienojums ir bezgalīgs, šķēlums ir galīgs, starpība (B\A) un simetriskā starpība ir bezgalīgas. Savukārt A\B – ir galīgs

|AxB| = |A||B|

2A- visas kopas A apakškopas.

1.7.3. Sanumurējamas kopas

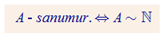
N, Z, Q – sanumurējamas

R – nesanumurējama

A – galīga, B – sanumurējama. =>

A – sanumurējama, B – sanumurējama => AUB – sanumurējams