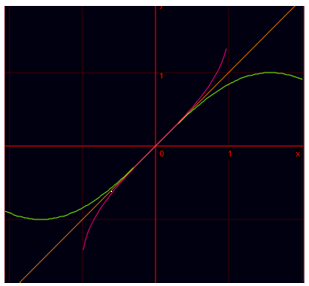
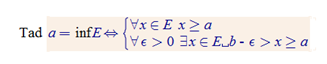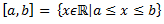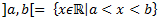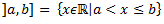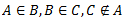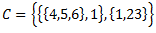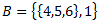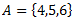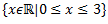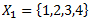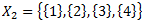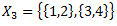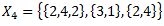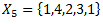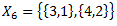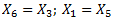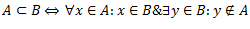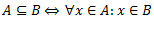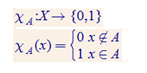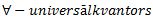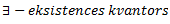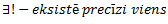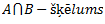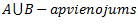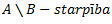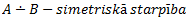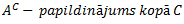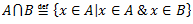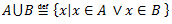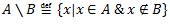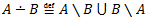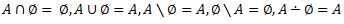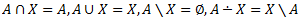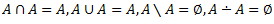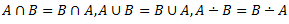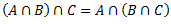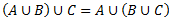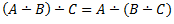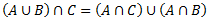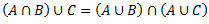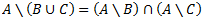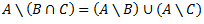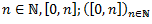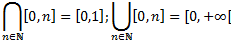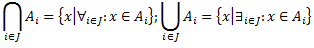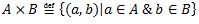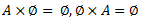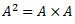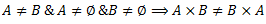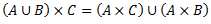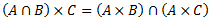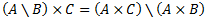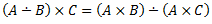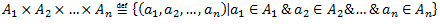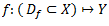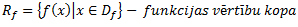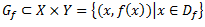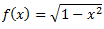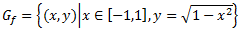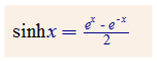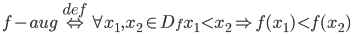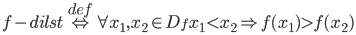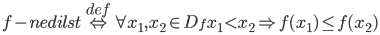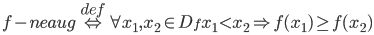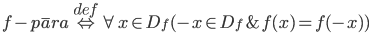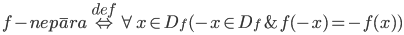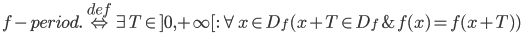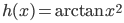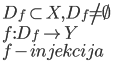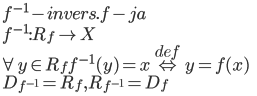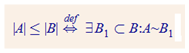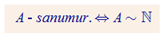Vēlviens ieraksts no sērijas “lekciju pieraksti”

2.1. Reālo skaitļu īpašības

Aksiomātiska def.

Īpašību grupas

I R ir sakārtota:

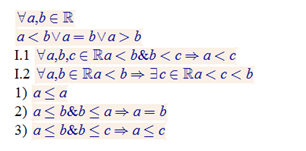
II Saskaitīšana

III Reizināšana

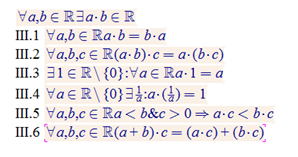
IV – Arhimēda īpašība

V- nepārtrauktība

2.2. Naturālu skaitļu kopa

2.3. Veselu skaitļu kopa

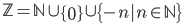
2.4. Racionālu sk. Kopa

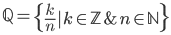
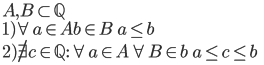
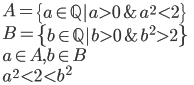
Alternatīva Q definīcija

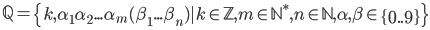
Iracionālu skaitļu kopa sastāv no bezgalīgiem bezperiodiskiem daļskaitļiem

2.5. Skaitļu kopas minimālais un maksimālais elements; infīms un suprēms

E – skaitļu kopa

2.5.1. Skaitļu kopas minimālais un maksimālais elements.

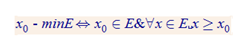
X₀ = minE

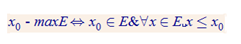
X₀ = maxE

Funkcijas max un min.

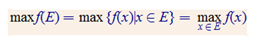
2.5.2. Ierobežotas un neierobežotas skaitļu kopas

Skaitļu kopa E ir ierobežota no augšas <=> Eksistē tāds M, ka visiem x no E x<= M

M – kopas E mažoranta <=> M no R un Visiem x no E x <= M

M – kopas E mažoranta => visiem M’ no R M’ > M => M’ – kopas E mažoranta

maxE – kopas E mažoranta

Skaitļu kopa E ir ierobežota no apakšas<=> Eksistē tāds m, ka visiem x no E x>= m

m – kopas E minoranta <=> m no R un Visiem x no E x >= m

m – kopas E minoranta => visiem m’ no R m’ < m => m’ – kopas E minoranta

minE – kopas E minoranta

Kopa E – ierobežota <=> (E ierobežota no apakšas & E ierobežota no augšas )

Ierob. no augšas – mažorējama

Ierob. no apakšas – minorējama

E – neierobežota no augšas <=> Visiem M no R Eksistē x no E : x>M

E – neierobežota no apakšas <=> Visiem m no R Eksistē x no E : x<M

E – ir neierobežota <=> ( E – neierobežota no augšas V E – neierobežota no apakšas )

2.5.3. Skaitļu kopas infīms un suprēms

Piemēri:

E = ]0,1[ – !eksistē minE , !eksistē maxE

0 – infīms == infE

1 – suprēms == supE

E = [0,1] – infE = minE = 0; supE = maxE = 1

N

1 = minN = infN

!Eksistē maxN, bet supN = +infinity

Ja eksitē minE => infE = minE

Ja eksistē maxE => supE = maxE

2.5.4. Skaitļu kopas infīma un suprēma eksistence

Katrai netukšai skaitļu kopai E eksistē infE un supE

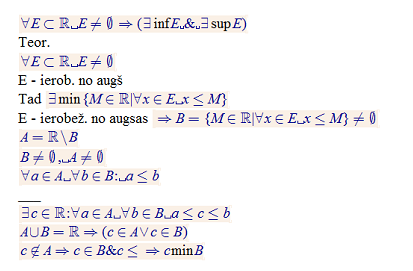
2.5.5 Skaitļu kopas infīma un suprēma raksturojums

Teor.

E – netukša ierobežota no augšas skaitļu kopa.

b – skaitlis

Teor.

E – netukša ierobežota no augšas skaitļu kopa.

a – skaitlis

Šodien pateicoties Pēterim uzgāju tādu lielisku resursu kā mathoverflow.net No turienes sekojošais:

There’s a thing called a meadow which is a (successful) attempt to make multiplicative inverses globally defined. What it does is instead of defining multiplicative inverses, it defines an operation M → M, x → x^-1 with the property not that xx^-1 = 1 but that xx^-1x = x. For any non-zero element then this agrees with the usual inverse but one can extend the inverse operation by defining 0^-1 = 0 and it works. I may be wrong, but I think that the result is that every field embeds in a meadow.

So providing you don’t claim that xx^-1 = 1 but rather xx^-1x = x then you are absolutely fine with 0^-1 = 0.

Ieraksts rakstu sērijā lekciju pieraksti.

1.1 Kopas jēdziens

Def: kopa

Ar vārdu kopa mat. saprot, tādu jēdzienu, kuram var viennozīmīgi pateikt, ka kāds elements tai pieder vai nepieder

Kopas parasti apzīmē ar lielajiem latīņu burtiem

N – naturālie

Z – veselie

Q – racionālie

R – reālie

C – kompleksie

– tukšā kopa

Intervāli:

(a,b) – vektors – nevis intervāls

3.kopas, kur

Uzdošanas veidi

• Ar elementu sarakstu (uzskaitot visus elementus)
  {a,b,c,d}
• Ar rakstīrīgo pazīmi (lielām/bezgalīgām kopām)

  

X – universs

Hi – kopas A harakteristiskā funkcija

1.2 Matemātiskās loģikas simboli

! (patiesībā izskatās, kā spoguļots lielais krievu G) – negācija

& – konjunkcija

V – disjunkcija

=> implikācija

<=> ekvivalence

1.3 Darbības ar kopām

�

A, B – kopas

1.3.5 Operāciju īpašības

Operācijas tiks veiktas, ar operācijām A,B,C, kuras ir universālkopas X apakškopas1.

2.

3.

4.

5.

6.

1.3.6 Kopas papildinājums

Kopas A papildinājums ir tie un tikai tie elementi, kas nepieder kopai A. (papildinājumam būtisks ir Universs, t.i. Kopa pret kuru tiek veikts papildinājums)

1.4 Kopu saimes

1.5 Dekarta reizinājums

1.5.1. Korteža jēdziens

Kortežs – sakārtota elementu virknīte (a,b,..)
(a,b) != {a,b} – iekš {a,b} secība nav svarīga, savukārt iekš korteža – secība ir svarīga.
Kortežu piemēri – Vektors, Matricas rinda, matricas kolonna.

1.5.2. Dekarta reizinājums

A,B – kopas

AxB = kopu A un B dekarta reizinājums

1.5.3. Dekarta reizinājuma īpašības

1.5 Funkcijas

1.6.1. Funkcijas vispārīga def.

X,Y – kopas, f – funkcija, Df – funkcijas definīcijas kopa

f ir likums, saskaņā ar kuru, katram funkcijas definīcijas kopas Df elementam x ir piekārtots viens kopas Y elements y, kuru apzīmē ar f(x) un sauc par funkcijas vērtību punktā x

X – funkcijas f starta kopa

Y – funkcijas f finiša kopa

f- var uzdot ar tabulu (ja X & Y ir galīgas kopas), grafiku vai analītiski (f(x) = x2)

Grafiks ir kopa:

f(x) = x2

1.6.2. Funkciju klasifikācija

• Visur definēa funkcija <==> D_f =X
  
• Sirjekcija <==> R_f = Y
  
• Injekcija <==> visiem y no R_f eksistē viens vienīgs x no D_f, tāds, ka y=f(x)
  
• Bijekcija <==> visur definēta funkcija & injekcija & sirjekcija
• Ja X = R, Y – R, – viena argumenta (reālas) funkcijas
• Ja X = Rⁿ, Y -R, – vairāku argumentu (reālu) funkcijas
  Ja X = Rⁿ, Y -R^k – vairāku argumentu vektorfunkcijas
  
• Ja X = C, Y – C, – kompleksā mainīgā funkcijas
  

  Ja Df = N – tad tā ir skaitļu virkne (a1,a2, …, an) – reāla viena argumenta funkciju speciālgadījums

Pamatelementārās funkcijas

1. Konstantes
   f(x) = C, kur C = ir reāls skaitlis – Df = R
2. Pakāpes f-jas
   f(x)=x^r Df – atkarīgs no r – ja r = 2 – Df = R, r = 1/2 – Df = R \ {0},
3. Eksponentfunkcijas
   f(x) = a^x
   a!= 1 & a>0
4. Logaritmiskās f-jas
   f(x)=log_a(x)
   a!= 1 & a>0
5. Trigonometriskās funkcijas
   f(x) = sin(x)| cos(x)| tg(x)| ctg(x)
6. Inversās trigonometriskās funkcijas
   f(x) = arcSin(x)|arcCos(x)|arcTg(x)|arcCtg(x)
7. Ciklometriskās funkcijas
   f(x) = sinh(x)|cosh(x)|tanh(x)|ctanh(x)

   
   Funkciju var iegūt no pamatelementārām funkcijām izmantojot galīgā skaitā operācijas + – * / kompozīcija

1.6.3. Viena reāla argumenta funkciju pamatīpašības

f- monotona <=> (f – nedilst) V (f – nedilst)

f – st. monotona <=> (f – aug) V (f -dilst)

f- ierobežota no augšas <=>

f- ierobežota no apakšas <=>

f – ierobežota <=> f – ierobežota no augšas & f -ierobežota no apakšas

1.6.4. Saliktas funkcijas jēdziens

Piemēri:

1.6.5. Inversās funkcijas jēdziens

X,Y – kopas

1.6.6. Attēli un pirmtēli

f(A) – kopas attēls

f-1(B) – kopas B pirmtēls

1.7. Kopas apjoms

1.7.1. Ekvivalentas kopas

A,B – kopas

1.7.2. Galīgas un bezgalīgas kopas

cardA, |A| – kopas elementu skaits

|tukša kopa| = 0

A ~ {1,2,3,…,n} => |A|= n

Kardinālskaitļi

Ja kopas A un B ir galīgas, tad apvienojums, šķēlums, starpība utt. ir galīgas kopas

Ja A un B ir bezgalīgas, tad apvienojums ir bezgalīgs, bet par pārējām op. neko nevar pateikt

Ja A – galīga un B bezgalīga, tad apvienojums ir bezgalīgs, šķēlums ir galīgs, starpība (B\A) un simetriskā starpība ir bezgalīgas. Savukārt A\B – ir galīgs

|AxB| = |A||B|

2A- visas kopas A apakškopas.

1.7.3. Sanumurējamas kopas

N, Z, Q – sanumurējamas

R – nesanumurējama

A – galīga, B – sanumurējama. =>

A – sanumurējama, B – sanumurējama => AUB – sanumurējams